
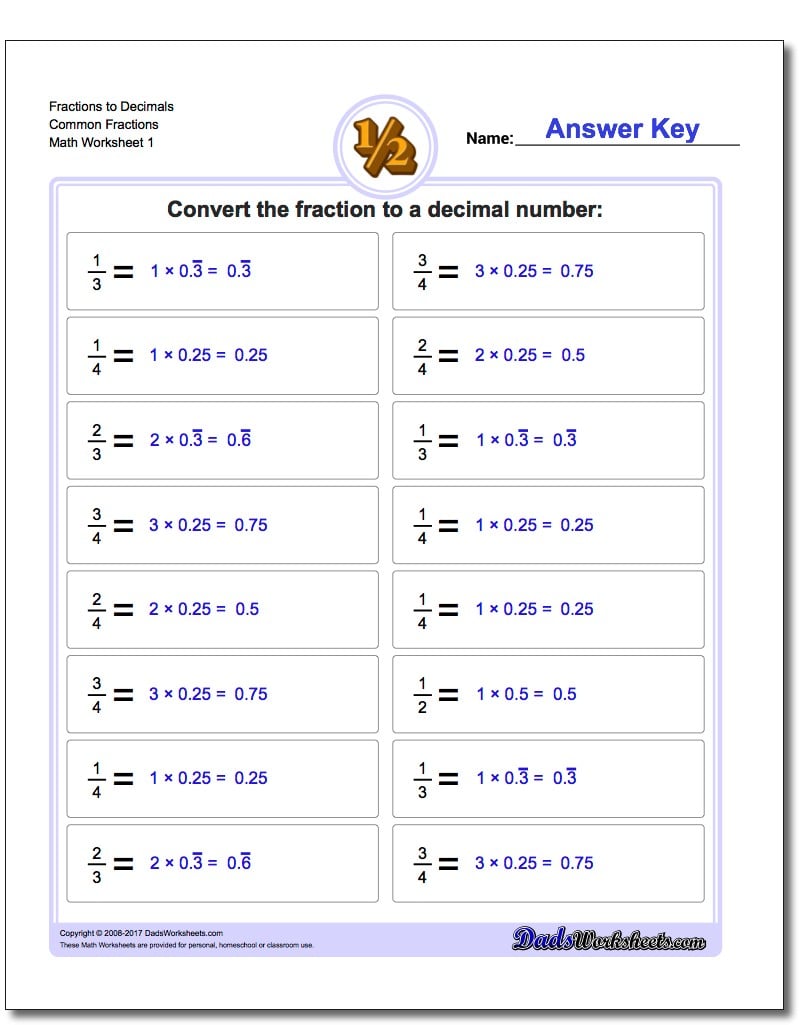
Is there a simpler one? Let’s take a look at the following method. This is the routine conversion process from decimal to fraction. So, the answer of 0.4 82 as a fraction is 239 495. Therefore, the numerator and denominator of the initial fraction are divided by 2 to get the final simplified fraction. Now, we have found that the greatest common divisor of 478 and 990 is 2. So, the greatest common divisor of 478 and 990 is 2. Next, we have to find the greatest common divisor of 478 and 990. The equation got from Step 1, divide both sides by 990 at the same time to get the initial fraction form.Ġ.4 82 = 478 990 Step 3. Convert integer equations into a fraction. Convert the decimal to an integer equation.Ġ.4 82, the decimal point is followed by an non-recurring decimal place of 4, and then followed by 2 repeating trailing decimal places of 82.
In the first step the previous total is always 0 because you are just starting. Step 2 As there is only 1 number after point so multiply 10 one time to both numerator and denominator. Starting from the left, you will be doubling the previous total and adding the current digit. Double dabble helps converting longer binary strings in your head and the only thing to remember is ‘double the total and add the next digit’. (Note that the digits 0 in the binary produced zero values in the decimal as well.)Īlso called doubling, this method is actually an algorithm that can be applied to convert from any given base to decimal. (1 * 2 3) + (0 * 2 2) + (1 * 2 1) + (0 * 2 0) For example, the decimal number 29.31 has 29 as integer part and 0.31 as a fractional part, separated by the decimal separator. Step 2: Represent the number in terms of its positions.Step 1: Write down (1010) 2 and determine the positions, namely the powers of 2 that the digit belongs to.

Now, let's apply these steps to, for example, the binary number above, which is (1010) 2 Step 3: Add the results and you will get the decimal equivalent of the given binary number. Continue doing this until you reach the most significant digit (MSB - the leftmost one). Step 2: Starting with the least significant digit (LSB - the rightmost one), multiply the digit by the value of the position. The second method is called double dabble and is used for converting longer binary strings faster. The first one uses positional representation of the binary, which is described above.
There are two methods to apply a binary to decimal conversion.
#Deciaml to integer fraction converter how to#
This means that every binary number could be represented as powers of 2, with the rightmost one being in the position of 2 0.Įxample: The binary number (1010) 2 can also be written as follows: (1 * 2 3) + (0 * 2 2) + (1 * 2 1) + (0 * 2 0) How to Convert Binary to Decimal As mentioned above, in the positional system of binary, each bit (binary digit) is a power of 2. In order to convert binary to decimal, basic knowledge on how to read a binary number might help.


 0 kommentar(er)
0 kommentar(er)
